Camille Carvalho
Research interests
Partial Differential Equations, Waves propagation, Electromagnetism, Scattering, Metamaterials and Plasmonics Modeling, Numerical Analysis, Simulation and scientific computing, Finite Elements Method, Spectral theory, waveguides, PMLs, Kondratiev theory, singularities, Boundary integral methods, Asymptotic analysis
Current research projects
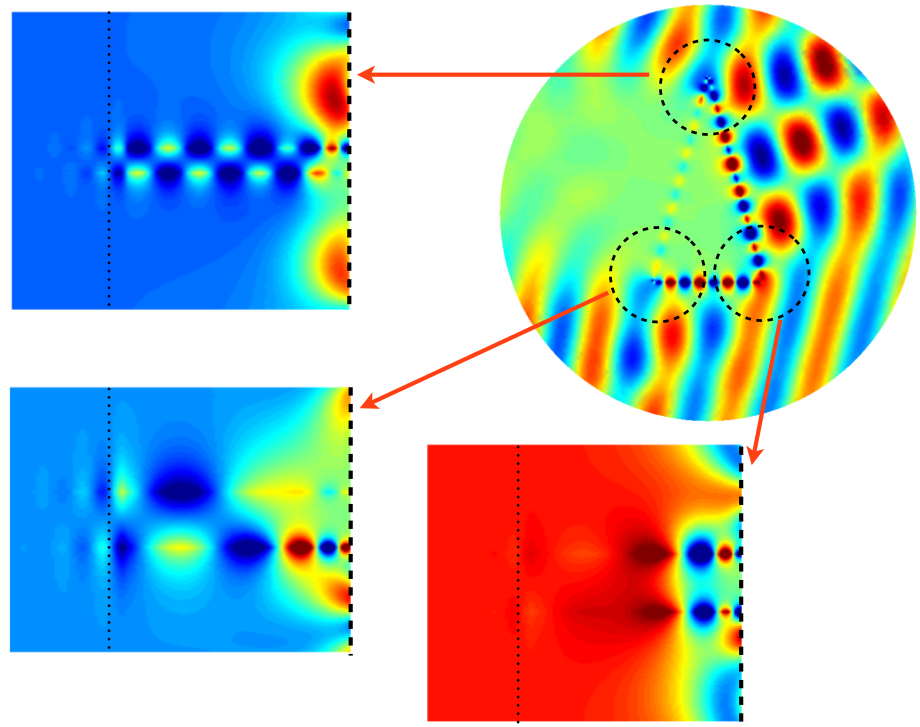
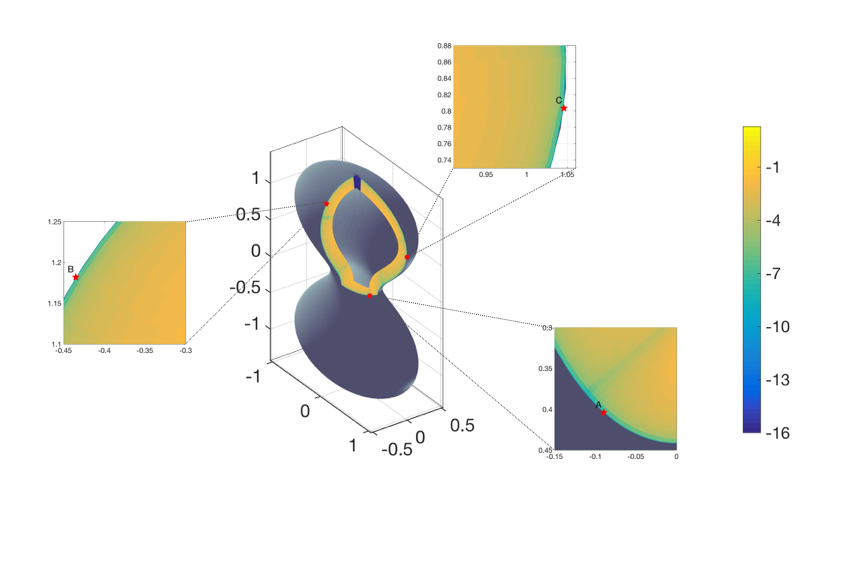
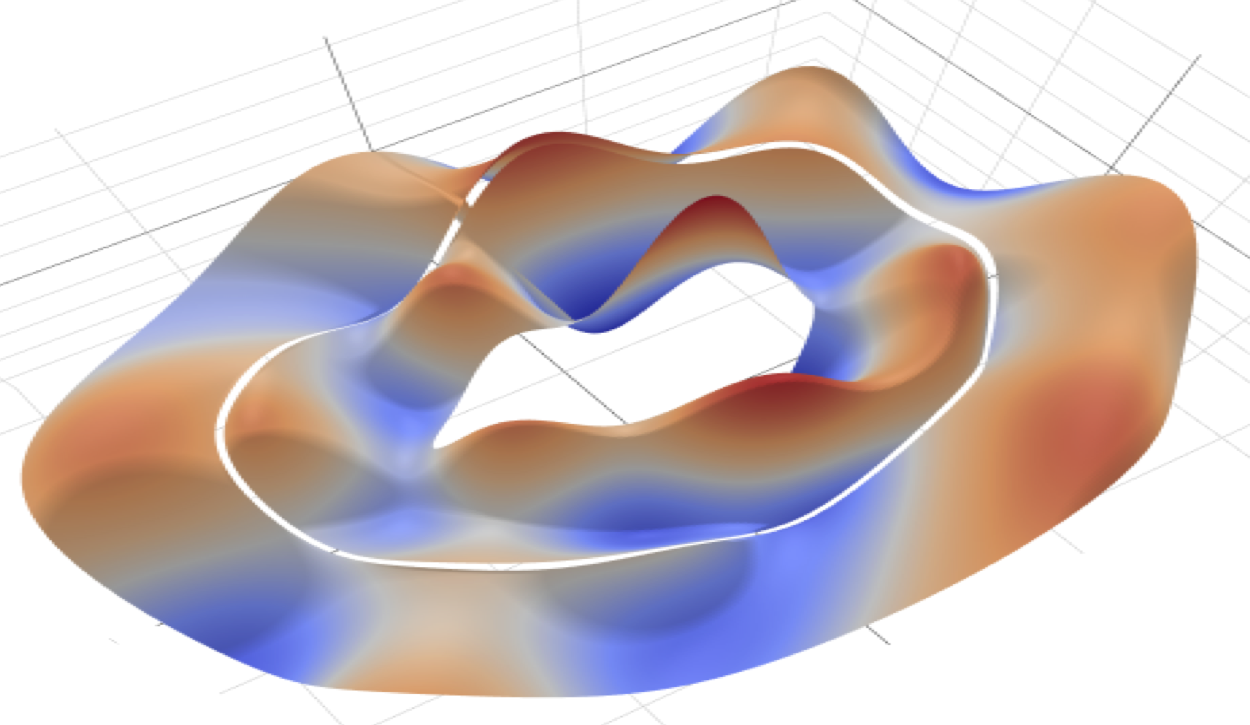
Click on the image to know more. An overview can be found [ here ]