Finite Element Method for Plasmonics
Plasmonic Structures
Plasmonic structures are made of a positive material (dielectrics) and a negative material (metals at optical frequencies, metamaterials). Surface electromagnetic waves called surface plasmons can appear at the interface.
Applications
Guiding and confining such particular waves in nanophotonic devices reveal a great interest to overcome the diffraction limit, in nanophotonic sensing and related applications.
Challenges
- Multiple scales
- Surface plasmons are very sensitive to the geometry (corners)
- Inaccurate predictions of the near field
- Hyper-oscillating singularities, called black-hole waves, appear at the corners
- Standard FEM fail due to spurious reflections
Novel Numerical Method using FEM
Mesh requirements to ensure FEM optimal convergence via the T-coercivity
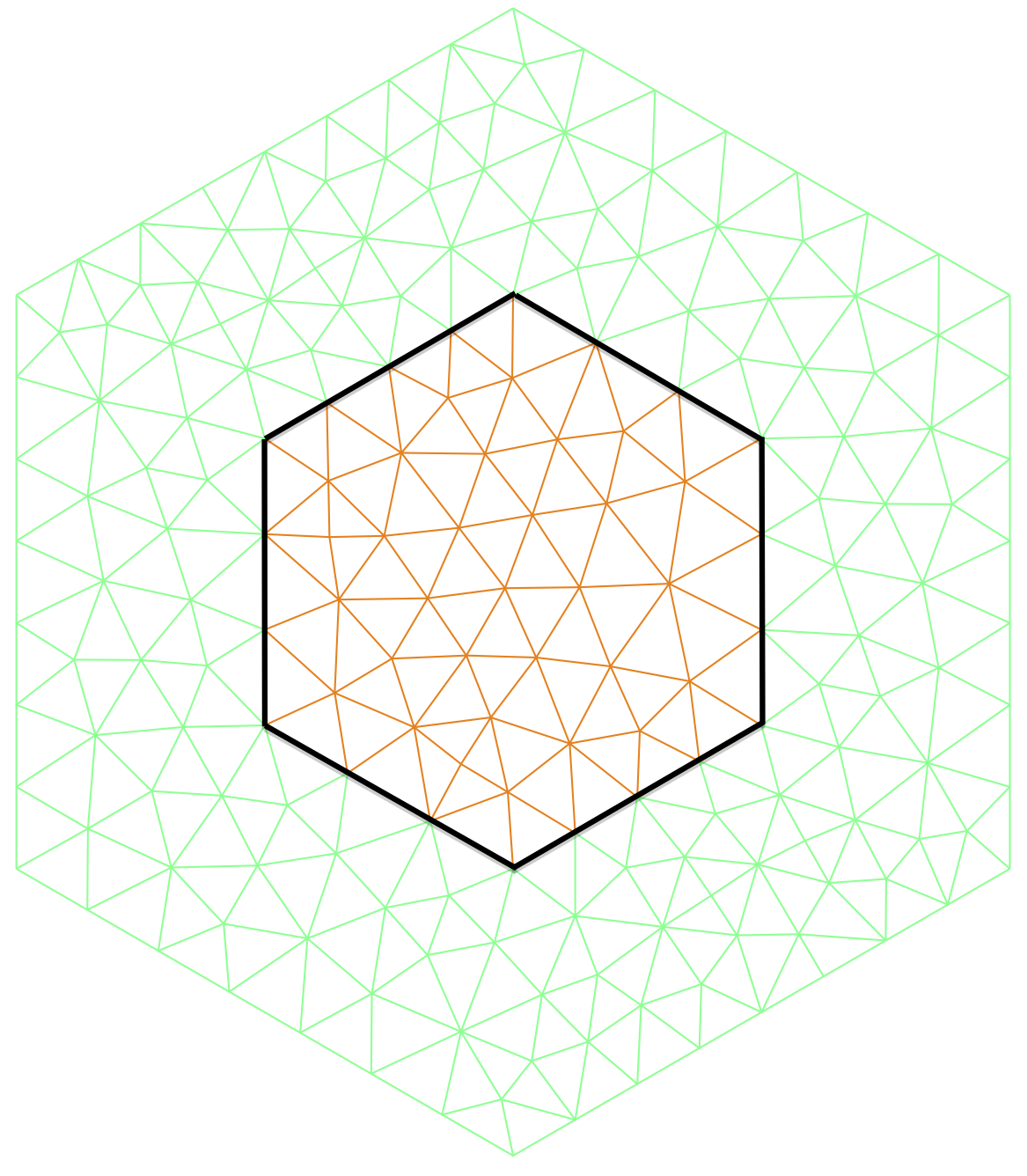
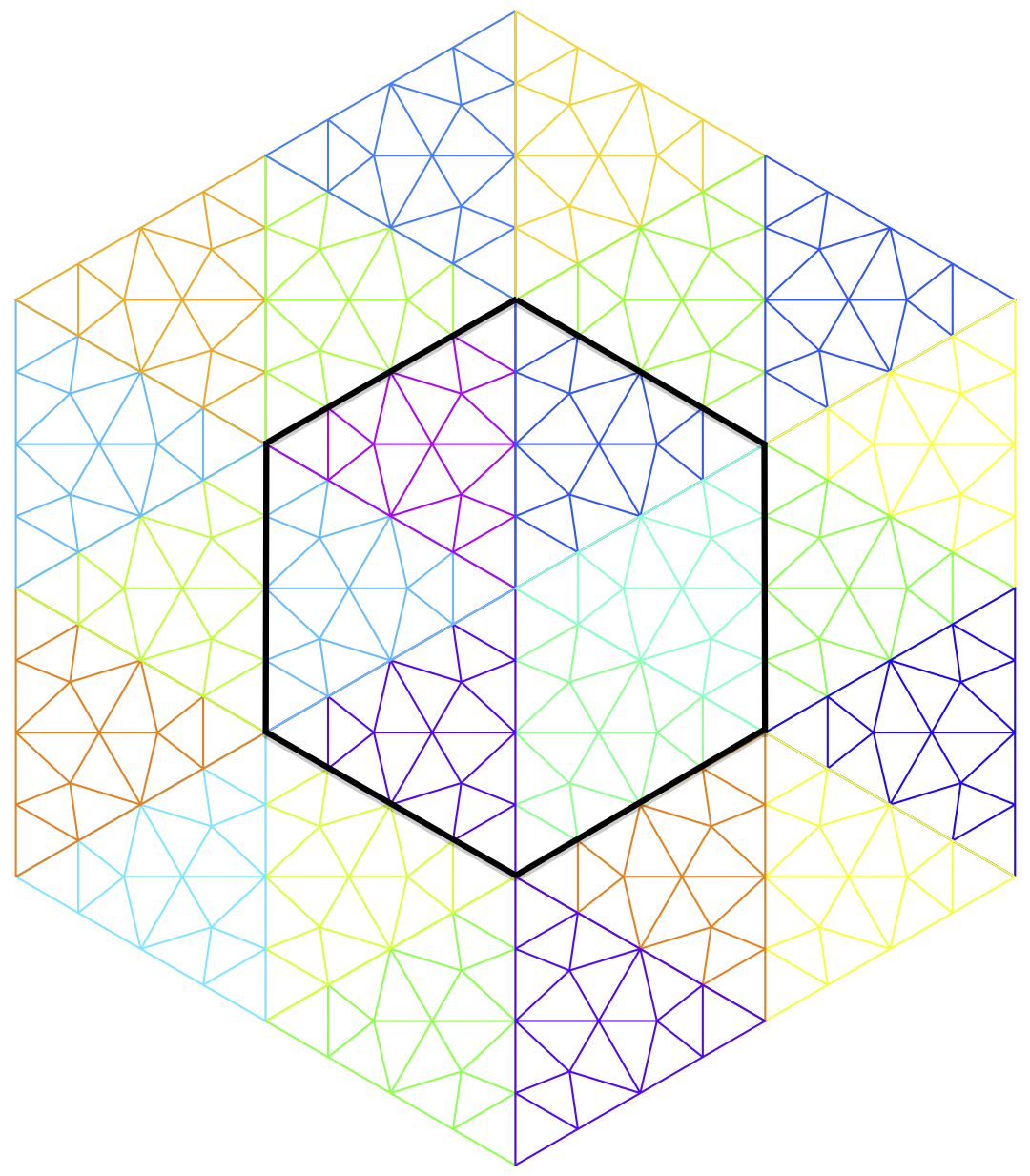
An hexagonal cavity with an hexagonal negative material inclusion. Left: standard mesh. Right: T-conforming mesh.
Use of Perfectly Matched Layers at the corners to capture the black-hole waves
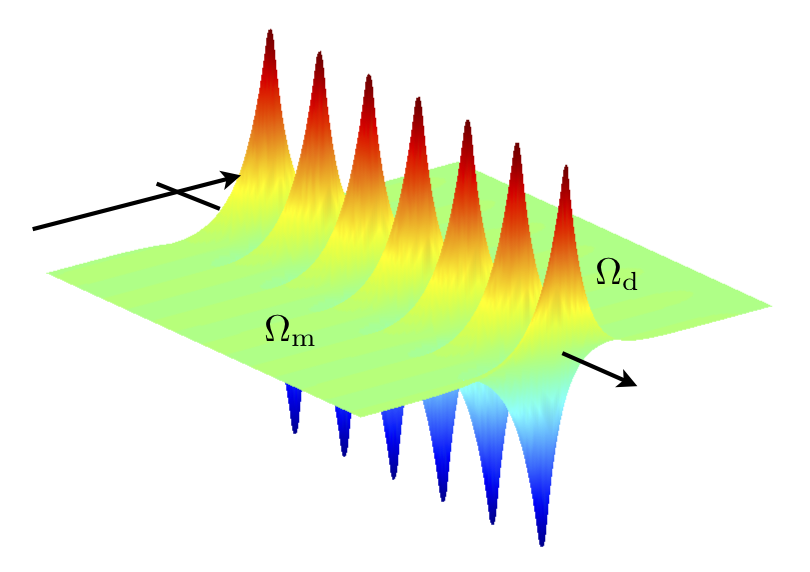
Scattering problem by a plane wave of a metallic inclusion. Top: standard FEM, spurious reflections at the corners (steady wave). Bottom: multi-scale method, the plasmons propagate towards the corners.
References
-
Mesh requirements for the finite element approximation of problems with sign-changing coefficients A.-S. Bonnet-Ben Dhia, C. Carvalho, P. Ciarlet Jr. Numerische Mathematik, pp 1-38, 2018.
-
Eigenvalue problems with sign-changing coefficients C. Carvalho, L. Chesnel, P. Ciarlet Jr. Compte Rendus Mathématiques, 355 (6), pp 671-675, 2017.
-
On the use of Perfectly Matched Layers at corners for scattering problems with sign-changing coefficients A.-S. Bonnet-Ben Dhia, C. Carvalho, L. Chesnel, P. Ciarlet Jr. Journal of Computational Physics, 322, pp 224-247, 2016.
Ongoing Projects
- T-conforming mesh generator
- Limiting Amplitude Principle